|
| since 2007.10.22 |
| last update 2015.02.20 |
|
|
| TopPage > 数学の基本を思い出さないとと思う今日このごろ |
| Contents |
| 微分の基本 |

|

|

| 極大/極小 |
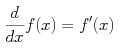 、
、


| 複合関数の微分 |


| 複素数の基本 |


|
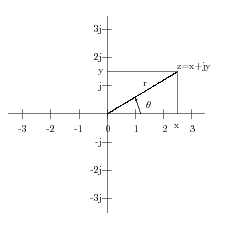
|
| 共役複素数 |
|
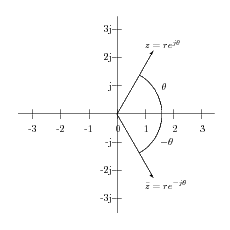
|
| 複素数の四則計算 |
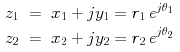
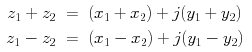


|
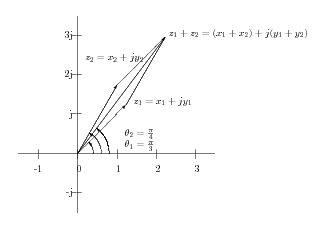
|



|
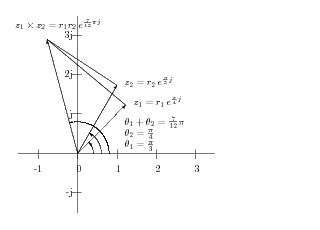
|
| 定数 |
| 因数分解[Factorize] |

| 三角関数[Trigonometric function] |

|

|
| 指数関数[Exponential function]・対数関数[Logarithmic function] |

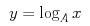
| 底が10 | :常用対数 |
| 底がe | :自然対数 |
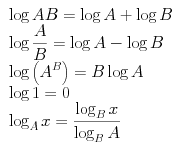
| ツェラーの公式[Zeller's congruence] |
| h = | ( | q + | ⌊ |
26(m+1) 10 |
⌋ | + K + | ⌊ |
K 4 |
⌋ | + | ⌊ |
J 4 |
⌋ | - 2J | ) | mod 7 |
| TopPage > 数学の基本を思い出さないとと思う今日このごろ |